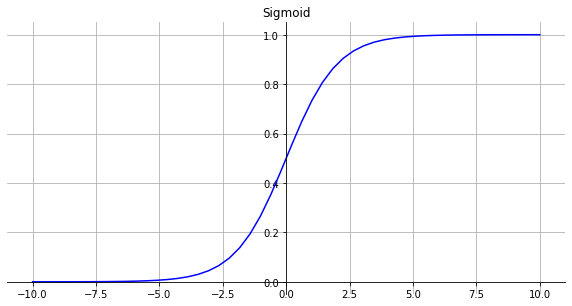
Sigmoid
函数
σ(x)=1+e−x1
导数
σ′(x)=σ(x)⋅(1−σ(x))
优点
- 函数是可微的。
- 梯度平滑。
- Sigmoid 函数的输出范围是 0 到 1,因此它对每个神经元的输出进行了归一化,课用于将预测概率作为输出的模型。
缺点
- 激活函数计算量大(在正向传播和反向传播中都包含幂运算和除法)
- 不是zero-centered
- 梯度消失
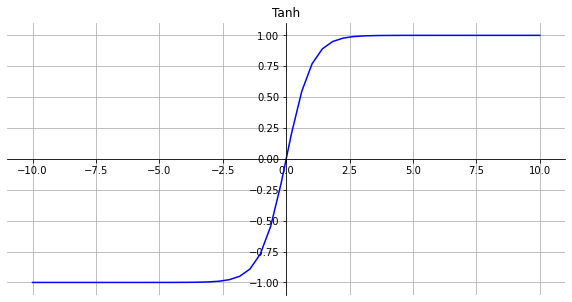
Tanh
函数
τ(x)=tanh(x)=ex+e−xex−e−x
导数
τ′(x)=1−τ2(x)
优点
- zero-centered
- 相比sigmoid梯度消失有所改善
- 梯度更大,容易收敛
缺点
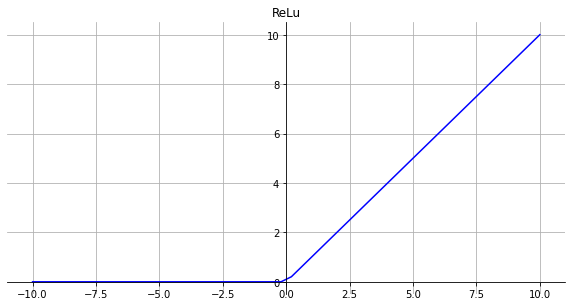
ReLu
函数
σ(x)=max(0,x)
导数
σ′(x)={01x<0x>0
优点
- 没有饱和区,不存在梯度消失问题,防止梯度弥散。
- 稀疏性。
- 计算简单。
- 收敛快。
缺点
- 会导致部分节点dead,当学习率变大时,dead节点更多
Softmax
函数
Softmax(xi)=∑jexjexi
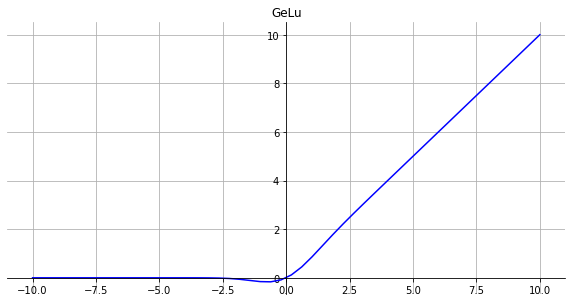
GeLu
函数
gelu(x)=xP(X≤x)X∼N(0,1)
实现
gelu(x)=21x(1+erf(2x)
1
2
3
4
5
| import numpy as np
import torch
def gelu(x):
cdf = 0.5 * (1.0 + torch.erf(torch.tensor(x) / np.sqrt(2.0)))
return x * cdf
|
导数
gelu′(x)=0.5tanh(0.0356774x3+0.797885x)+(0.0535161x3+0.398942x)sech2(0.0356774x3+0.797885x)+0.5
优点
- GeLu可以看作是dropout和relu的结合
- 按照正态分布去dropout节点
缺点