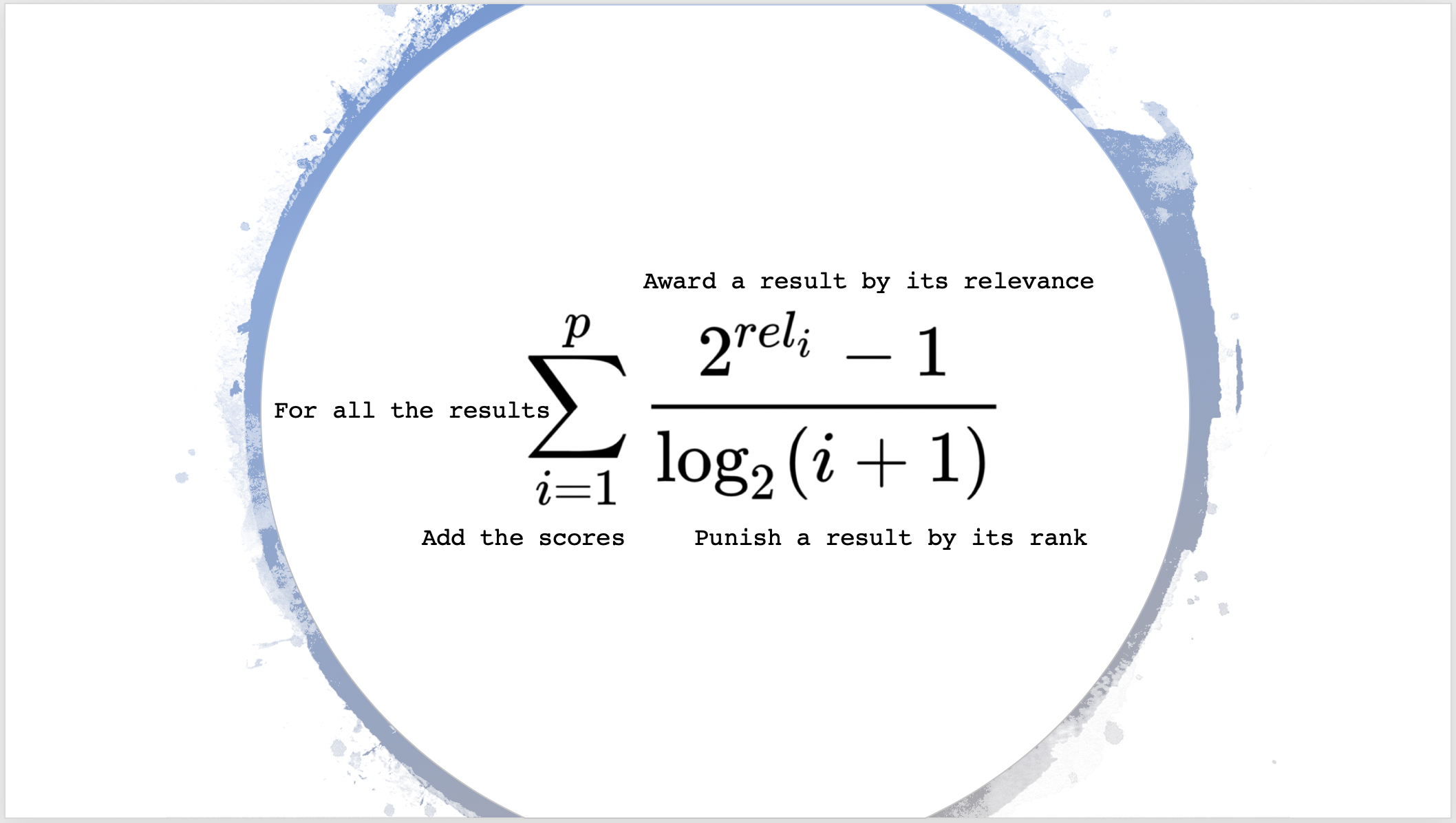大模型评估数据集
基础常识推理
BoolQ
BoolQ is a question answering dataset for yes/no questions containing 15942 examples. These questions are naturally occurring ---they are generated in unprompted and unconstrained settings. Each example is a triplet of (question, passage, answer), with the title of the page as optional additional context. The text-pair classification setup is similar to existing natural language inference tasks.
PIQA(Physical Interaction: Question Answering)
The dataset contains 16,000 examp ...
GPT Series
GPT1
Improving Language Understanding by Generative Pre-Training
前言
将之前词向量等无监督称之为Semi-supervised learning,将GPT1这种无监督称之为Unsupervised pre-training(作为Semi-supervised learning的子集)
Framework
Unsupervised pre-training
给定一个句子U=(ui)U=(u_i)U=(ui),极大似然
L1(U)=∑ilogP(ui∣ui−k,…,ui−1;Θ)L_1(\mathcal{U})=\sum_i \log P\left(u_i \mid u_{i-k}, \ldots, u_{i-1} ; \Theta\right)
L1(U)=i∑logP(ui∣ui−k,…,ui−1;Θ)
kkk为上下文窗口大小
Supervised fine-tuning
......
...
L3(C)=L2(C)+λ∗L1(C)L_3(\mathcal{C})=L_2(\mathcal{C} ...
Tokenizer中的Subword算法
说起Tokenizer,不得不先介绍一下Subword
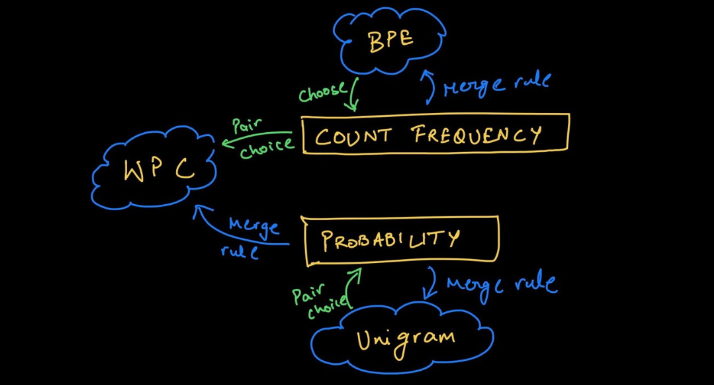
目前常见的Subword算法包括BPE、WordPiece、Unigram、SentencePiece及相关变体
BPE
BPE —— Byte-Pair Encoding 是一种压缩算法,BPE算法按如下步骤生成词表:
将语料按字符切分,并在单词末尾加以</w>标记。
确定期望的词表大小
统计每两个subword的共现频率,选择共现频率最大的一对subword合并生成新的subword
重复上一步知道subword个数满足期望的词表大小或共线频率最大为1时停止
12345678910111213141516171819202122232425262728import re, collectionsdef get_stats(vocab): pairs = collections.defaultdict(int) for word, freq in vocab.items(): symbols = word.split() for i in range(len(symbol ...
推荐系统常用指标
推荐系统常用指标
MAP
MAP —— Mean Average Precision, 即对多个AP求平均。
AP定义如下:
AP=∑knP(k)×rel(k)∑knrel(k)\mathrm{AP}=\frac{\sum_{\mathrm{k}}^{\mathrm{n}} \mathrm{P}(\mathrm{k}) \times \operatorname{rel}(\mathrm{k})}{\sum_{\mathrm{k}}^{\mathrm{n}} \operatorname{rel}(\mathrm{k})}
AP=∑knrel(k)∑knP(k)×rel(k)
其中,rel(k)\operatorname{rel}(\mathrm{k})rel(k)表示当第k个预测值与ground truth相关(相同)时为1,否则为0;P(k)\mathrm{P}(\mathrm{k})P(k)表示前k个预测值中相关的占比。
示例:
预测序列e,b,a,d,c ; ground truth为a,b,c,d,e ,则第2个和第4个预测值与gt匹配,AP则为:
AP=12+242 ...
新机器配置环境
创建用户
12useradd -d ${home path} -m ${user name} // 创建用户并指定home目录,若不存在则创建-msudo passwd ${user name} // 给用户设置密码
给用户设置zsh
参考 https://www.haoyep.com/posts/zsh-config-oh-my-zsh/
123456789101112sudo apt install zsh -ychsh -s /bin/zshsh -c "$(wget -O- https://install.ohmyz.sh/)" // 安装oh-my-zshgit clone --depth=1 https://github.com/romkatv/powerlevel10k.git ${ZSH_CUSTOM:-$HOME/.oh-my-zsh/custom}/themes/powerlevel10k // 安装powerlevel10k主题vim ~/.zshrcZSH ...
matplotlib
matplotlib
常用代码段
123fig = plt.figure() # an empty figure with no Axesfig, ax = plt.subplots() # a figure with a single Axesfig, axs = plt.subplots(2, 2) # a figure with a 2x2 grid of Axes
docker 配置
/etc/docker/daemon.json 相关配置
Dockerfile中执行apt update报错Temporary failure resolving
Temporary failure resolving是指地址解析失败
检查地址是否有问题,如果地址无误,/etc/docker/daemon.json中添加如下dns服务器
12345{ "dns": [ "8.8.8.8" # Google DNS server ]}
L1正则化与L2正则化的区别
结论
正则化都可以防止模型过拟合。
L1正则化更容易获得为0得解,即权重更倾向为稀疏,常用于进行特征选择。
L2正则化使得解的趋向0而不为0(不因正则化为0)。
假定参数为 www ,loss函数为 L(w)L(w)L(w) ,则包含L1正则化的目标函数为
F=L(w)+λ∣w∣ F = L(w) + \lambda \lvert w \rvert
F=L(w)+λ∣w∣
在 w=0w=0w=0 处的导数为
∂F∂w∣w=0+=∂L(w)∂w+λ \left.\frac{\partial F}{\partial w}\right|_{w=0^{+}} = \frac{\partial L(w)}{\partial w} + \lambda
∂w∂F∣∣∣∣∣w=0+=∂w∂L(w)+λ
∂F∂w∣w=0−=∂L(w)∂w−λ \left.\frac{\partial F}{\partial w}\right|_{w=0^{-}} = \frac{\partial L(w)}{\partial w} - \lambda
∂w∂F∣∣∣∣∣w=0−=∂w∂L ...
Normalization
之前有大概看过Normalization,了解了LN和BN的区别,恰好前段时间在面试中被问到,发现之前了解的还是太模糊了,所以又深入学习了一些,顺便写了个笔记。
什么是Normalization
一种使神经网络特征保持固定分布的运算
Normalization是如何计算的
y=x−E[x]Var[x]+ϵ∗γ+β y = \frac{x - \mathrm{E}[x]}{ \sqrt{\mathrm{Var}[x] + \epsilon}} * \gamma + \beta
y=Var[x]+ϵx−E[x]∗γ+β
以下是自己通过均值和方差做的对比实验,可以看到结果是一样的。但实际上LN在使用时大部分参数会采用默认值,即elementwise_affine=True以及eps=1e-5,只是那样我们去对比就过于麻烦,理解就好
12345678910111213import torchimport torch.nn as nn# Official NLP Examplebatch, sentence_length, embedding_dim = 20, 5, 10embedd ...
algorithms
动态规划
通过缓存子问题的结果来递推解决目标问题的解决方案
判断是否为动态规划问题的依据
是否存在子问题的局部最优解为全局最优解的局部解
是否可以找到状态(子问题与目标问题的规模n这个变量)
是否存在状态转移方程(递推公式,即子问题规模从n到n+1,最优解的关系,例如f(n+1)=f(n)+2)
12class A(object): ...