LLM 训练步骤
前两部和以前的语言模型无异,我们以ChatGPT的博客,看一下RLHF做了些什么
RLHF——PPO与LM的结合
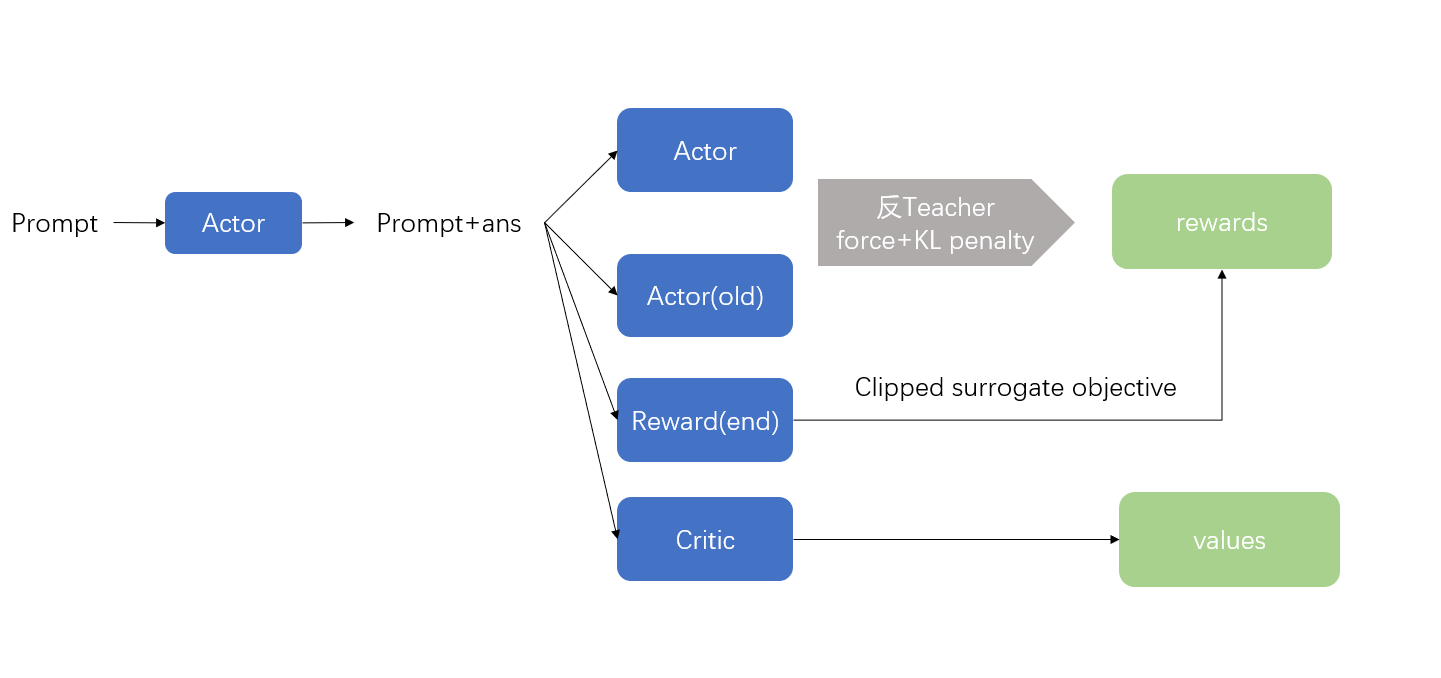
PPO属于Actor-Critic架构,Actor即策略也就是LLM本身,那么我们需要一个能对Actor输出结果进行打分的Critic值函数,因此我们先介绍Critic部分,该部分我们称之为Reward Model的训练,以dschat为例
Reward Model
Backbone采用LLM-base部分(即预训练后、监督微调前),输出头表示每个Token对应的V值。模型loss为pairwise loss
1
| loss -= F.logsigmoid(c_divergence_reward - r_divergence_reward).mean()
|
并且以last token作为终止奖励,根据模型可选的增加一个新的token
PPO
- 以
KL Penalty Coefficient加上Reward模型的end reward作为额外的奖励值(个人感觉不是很必要,同时用了clipped advantage)
- 计算actor的输出分布时,要反teacher force,以及只取对应token的logist(模型输出为length * vocab_size -> length * 1)而不要使用池化
- end reward需要clip
Generalized Advantage Estimation(广度优势估计)
Advantage function
A(st,a)=Q(st,a)−V(st)A(st,a)=rt+γV(st+1)−V(st)
由于语言模型生成episode(Prompt+ans)视为MC采样,存在方差较大的问题,TD采样又存在偏差较大的问题,因此提出GAE(等价于TD(n)采样)平衡方差和偏差。而MC可看作无限大步数的TD采样,又称 TD(λ)
A(st,a)=rt+γV(st+1)−V(st)A(st,a)+γA(st+1,a)=rt+γrt+1+γ2V(st+2)−V(st)Σn=0∞γnA(st+n,a)=Σn=0∞γnrt+n+γ∞V(st+∞)−V(st)Σn=0∞γnA(st+n,a)=Σn=0∞γnrt+n−V(st)
优势函数估计的方差随步长增大而增大,偏差随步长的增大而减小,因此对不同步长的估计进行加权求和,为简化方便,权重为 (1−λ)λn
AGAE =(1−λ)A(st,a)+(1−λ)λ(A(st,a)+γA(st+1,a))+⋯+(1−λ)λnΣn=0∞γnA(st+n,a)=(1−λ)[A(st,a)(1+λ+⋯+λn)+γA(st+1)(λ+⋯+λn)+⋯+γnA(st+n,a)λn]=(1−λ)[A(st,a)(1−λ1)+λγA(st+1,a)(1−λ1)+⋯+λnγnA(st+∞,a)(1−λ1)]=Σn=0∞λnγnA(st+n,a)
根据 λ 的取值取舍方差和偏差。
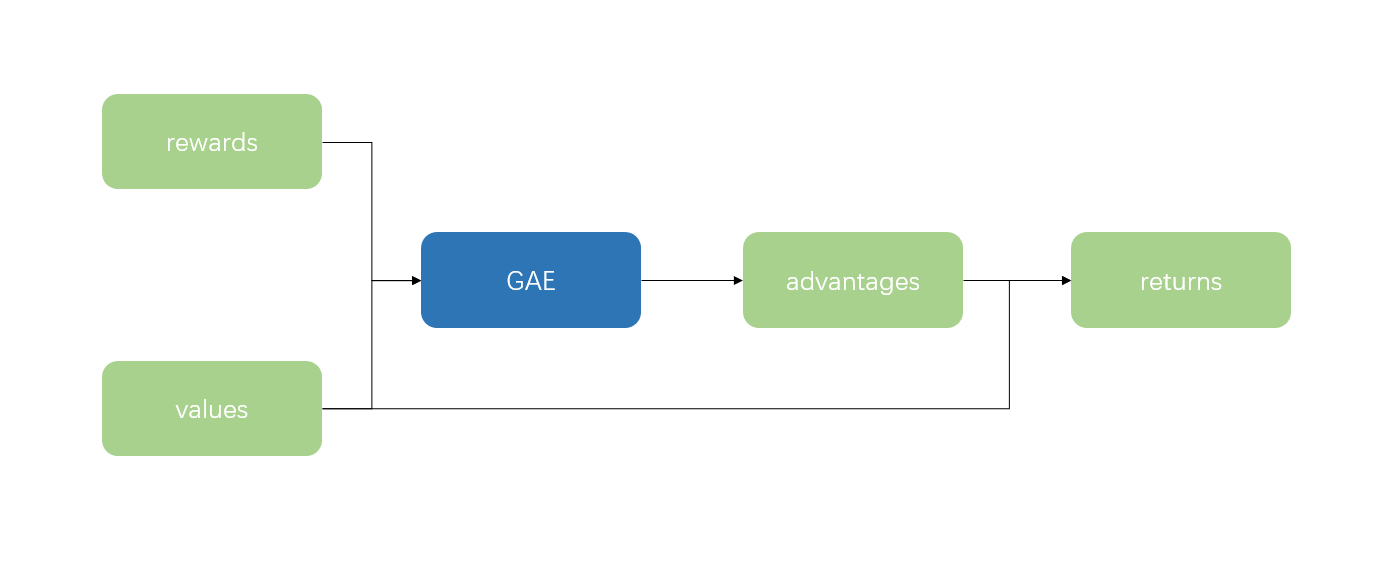
通过r值和V值计算出advantage,加上V值作为return。其中advantage用来指导actor优化,return用来指导critic优化。
- 为简化计算,通常倒序计算 AtGAE=A(st,a)+λγAt+1GAE 即 AtGAE=rt+γV(st+1)−V(st)+λγAt+1GAE
- 终止奖励对应位置的V值为0
- 在计算actor loss和critic loss的时候,对应advantage和return一般都做clip处理
Importance Sampling(重要性采样)
LM做PPO时,因on-policy耗时太久,通常采用off-policy方式。因此用来优化actor的episode并不全部符合actor的分布。此时我们需要用到重要性采样来修正优势函数估计。
Ex∼p[f(x)]=∫f(x)p(x)dx=∫f(x)q(x)p(x)q(x)dx=Ex∼q[f(x)q(x)p(x)]
对优势函数估计进行重要性采样修正作为actor的loss,critic的loss为return和V值的MSE。